誕生日のパラドックス

誕生日のパラドックスとは、

大体どれくらいの確率になると思いますか？

クラスではなかったとしても、LINEやインスタの友だちを上から40人見たときに誰か同じ誕生日の人がいる確率でも構いません。

.

.

.

.

.

.

.

.

.

答えはなんと約89.12%です。

自分の感覚は正しかったですか？
こんなに高いとは思ってもいなかったのではないでしょうか。

この感覚のギャップを誕生日のパラドックスと呼びます。

（正確にはパラドックス、つまり、「矛盾」ではありませんが、誕生日のパラドックスと呼びます。）

誕生日のパラドックスの確率の計算方法

誕生日のパラドックスの計算方法は高校の数学A程度の内容で簡単に説明できます。

と考えられるため、

2人の中で誰かしら誕生日が同じになる確率は

$$ 1 – \frac{365}{365} × \frac{364}{365} ≒ 0.27 \% $$
となり、

3人の中で誰かしら誕生日が同じになる確率は

$$ 1 – \frac{365}{365} × \frac{364}{365} × \frac{363}{365} ≒ 0.82 \% $$

4人の中で誰かしら誕生日が同じになる確率は

$$ 1 – \frac{365}{365} × \frac{364}{365} × \frac{363}{365} × \frac{362}{365} ≒ 1.64 \% $$

と表すことができます。



この計算をしていくと

23人の中で誰かしら誕生日が同じになる確率は

$$ 1 – \frac{365}{365} × \frac{364}{365} ・・・・・・× \frac{343}{365} × \frac{342}{365} ≒ 50.73 \% $$

40人の中で誰かしら誕生日が同じになる確率は

$$ 1 – \frac{365}{365} × \frac{364}{365} ・・・・・・× \frac{327}{365} × \frac{326}{365} ≒ 89.12 \% $$

となります。
なんと57人で約99.01%となるため、TwitterやInstagramのフォロワーを57人テキトーに選んだら誰かしら誕生日が同じである確率は99%となります。


なお、グラフにするとこのような形になります。
　

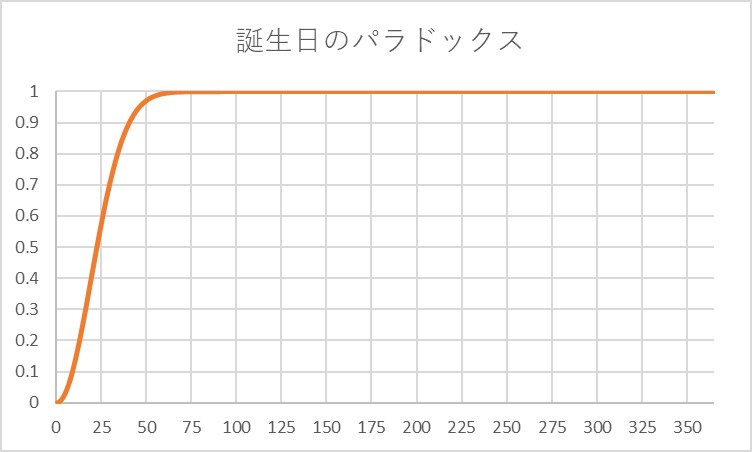
信じられないかもしれませんが、実際にExcel等でグラフを作成するとこのような形になります。

なぜパラドックスなのか

パラドックスとは矛盾という意味ですが誕生日のパラドックスは何も矛盾はしていません。


自分の感覚と結果が異なるので矛盾しているように感じるという意味でパラドックスという言葉が使われています。


また、自分と同じ誕生日の人がいる確率はこれほど高くないため自分と同じ誕生日の人がいる確率と混同して考えてしまうことが多いようです。あくまでも、誰かと誰かの誕生日が同じである確率です。

つまり、

「え！〇〇と△△は誕生日が同じなんだね！偶然ってすごい！」

ではないのです。

誕生日の同じ人が誰もいない確率の方が圧倒的に低い。

誰も同じ誕生日のペアがいないときに、偶然ってすごいと感じろ。

自分と同じ誕生日の人がいる確率の計算方法

ちなみに、自分と同じ誕生日の人がいる確率となると計算はかなり変わります。
40人(自分含む)の中で自分と同じ誕生日の人がいる確率は約10.39%です。こちらは自分の感覚と近い数値なのではないでしょうか。それとも、まだ高く感じるでしょうか。

一応こちらも解説すると

であるため、40人の場合は


$$ 1 – (\frac{365}{365})^{39} ≒ 10.39 \% $$

となります。

グラフにするとこのような形になります。

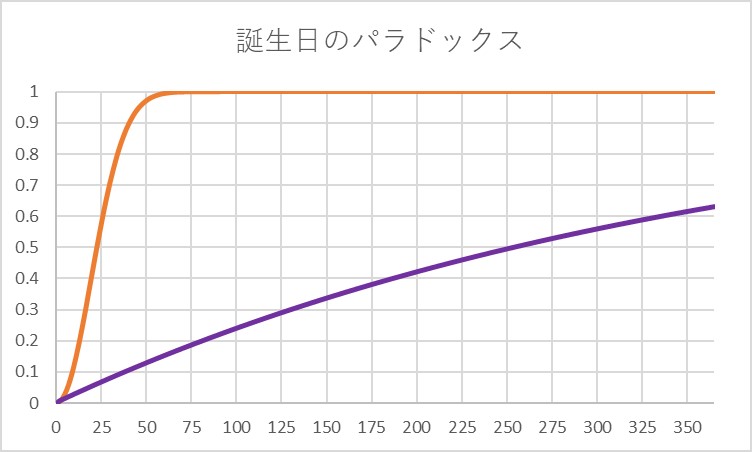
紫色の方のグラフが自分と同じ誕生日の人がいる確率になります。
先程のグラフとは形が変わっていますね。
また、365人いても自分と誕生日が同じな人のいる確率は100%にはなりません。

この計算は紛れもない事実であり、これからも一生変わりません。

「今まで自分と同じ誕生日の人と会ったことないんだよね」

本当ですか？
252人の人と会えば、自分と同じ誕生日の人のいる確率は50%を超えます。
839人の人と会えば、自分と同じ誕生日の人のいる確率は90%を超えます。

同じ誕生日の人と会ったことないんじゃなくて、人と会ったことないの間違いでは？